Filtraggio dei segnali (usa il Signal Processing Toolbox)
Introduzione
Non è questa la sede opportuna per sviluppare la teoria dei filtri digitali. A noi basterà sapere che un filtro digitale (chiamato anche filtro numerico) è un filtro che permette di compiere alcune funzioni matematiche su campioni di segnali in ingresso, modificando alcuni aspetti del segnale stesso.
Chi non conosce la trasformata di Laplace può saltare direttamente al paragrafo FILTRAGGIO.
Appunti sparsi di teoria
Chi invece conosce le basi della teoria dei sistemi sa che in generale per determinare l'uscita y(t) di un sistema a partire dall'ingresso x(t) è necessario usare la trasformata e l'antitrasformata di Laplace:
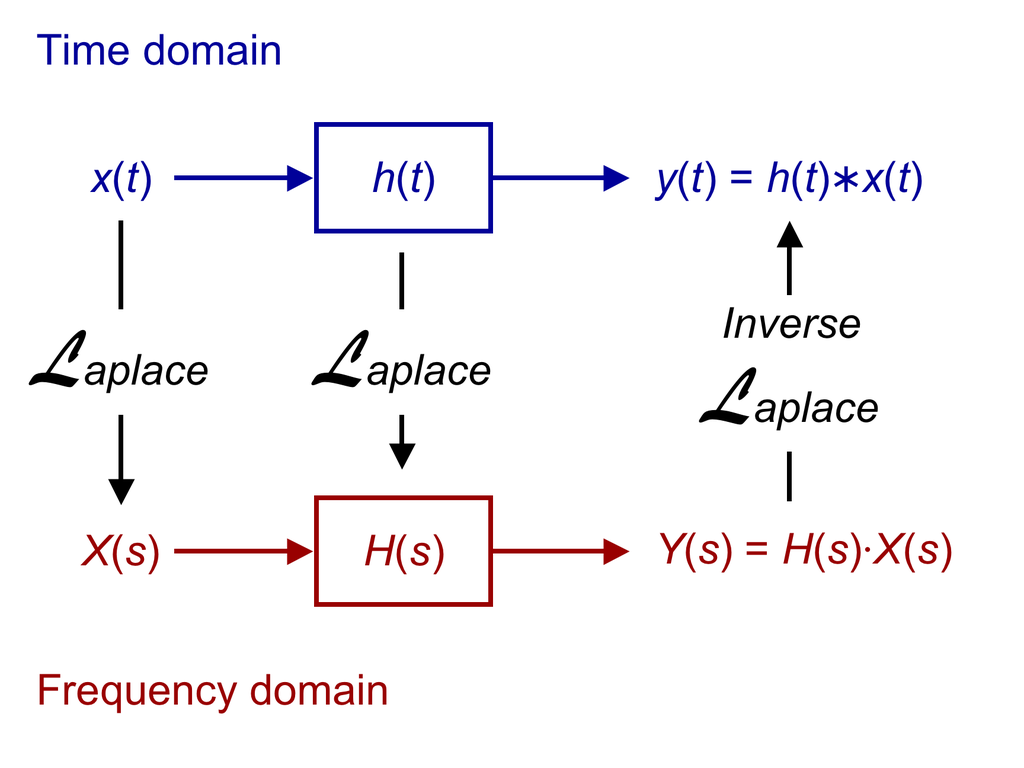
in particolare, per prima cosa si applica la trasformata di Laplace all'ingresso x(t) e alla risposta impulsiva del sistema h(t) per portarsi ad una relazione del tipo
Y(s) = H(s) X(s)
dove:
- Y(s) è la trasformata di Laplace dell'uscita
- H(s) è la trasformata di Laplace della risposta impulsiva che prende il nome di funzione di trasferimento e ha la forma
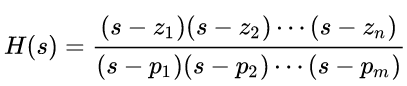
- X(s) è la trasformata di Laplace dell'ingresso
Una volta determinata Y(s) si applica la trasformata inversa di Laplace e si trova l'andamento y(t) dell'uscita.
La trasformata zeta unilatera è la trasformata di Laplace di un segnale campionato in modo ideale con la sostituzione:
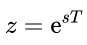
dove T = 1/fc è il periodo di campionamento e fc è frequenza di campionamento (misurata in campioni per secondo o in hertz).
Applicando la trasformata z si arriva ad una relazione tra la trasformata z dell'uscita Y(z) e dell'ingresso X(z) del tipo:
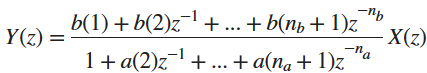
(si osserva che sostituendo la lettera "s" alla lettera "z" e cambiando il segno agli esponenti si trova l'espressione di una funzione di trasferimento).
A differenza dei sistemi continui, nei sistemi discreti è possibile antitrasformare nel caso generico e determinare una relazione tra i campioni dell'uscita e i campioni dell'ingresso:
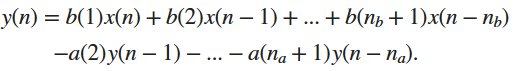 (1)
(1)
La relazione ci permette di capire che per determinare l'n-esimo campione dell'uscita y(n ) è necessario tener conto:
- dell'ennesimo campione dell'ingresso x(n )
- dei precedenti nb campioni dell'ingresso x(n-1), x(n-2), ... , x(n-nb)
- dei precedenti na campioni dell'uscita y(n-1), y(n-2), ... , y(n-na) (già calcolati precedentemente)
Progettare un filtro significa trovare i coefficienti b(1), b(2), ... , b(nb+1), a(2), a(3), ... , a(n-na) che operano il filtraggio desiderato.
In primo luogo si osserva che la parte a destra dell'equazione (1) si può dividere in due parti:
- quella che coinvolge i campioni dell'ingresso x(n ), x(n-1), x(n-2), ... , x(n-nb) che prende il nome di parte non ricorsiva del filtro
- quella che coinvolge i campioni dell'uscitay(n-1), y(n-2), ... , y(n-na) che prende il nome di parte ricorsiva del filtro
I filtri FIR (finite impulse response) sono filtri che hanno solo la parte non ricorsiva, ovvero i coefficienti b(1), b(2), ... , b(nb+1) diversi da zero, mentre a(2) = a(3) = ... = a(n-na) = 0.
I filtri IIR (infinite impulse response) hanno invece entrambe le parti, ricorsiva e non ricorsiva.
I filtri FIR sono molto apprezzati perché sono intrinsecamente stabili. Possono essere progettati in modo da avere una fase lineare che introduce un ritardo nel segnale filtrato senza alterare la conformazione della forma d’onda. Tuttavia, questi filtri possono avere lunghe risposte transitorie e, in certe applicazioni, possono rivelarsi abbastanza costosi in termini computazionali.
I filtri IIR sono utili soprattutto quando le risorse computazionali assumono un ruolo di primaria importanza. Tuttavia, i filtri IIR, stabili e causali, non hanno una fase perfettamente lineare. I metodi di progettazione dei filtri basati su IIR comprendono Butterworth, Chebyshev (Tipo I e Tipo II) e quello ellittico.
Per una trattazione più approfondita si rimanda alla letteratura specializzata come Oppenheim, Alan V.; Schafer, R. W.; and Buck, J. R., Discrete-time signal processing, Upper Saddle River, N.J., Prentice Hall, 1999, ISBN 0-13-754920-2.
Il modo più semplice per trovare i coefficienti in Matlab è utilizzare la funzione fir1() (quindi si progetterà un filtro FIR) mentre per eseguire il calcolo indicato in (1) è possibile utilizzare la funzione filter().
Filtraggio
L'operazione di filtraggio avviene dimensionando il filtro tramite la funzione fir1() e poi eseguendo il filtraggio dei campioni tramite la funzione filter().
La funzione fir1() viene utilizzata nel seguente modo:
b = fir1(n,Wn,ftype)
dove:
- n è l'ordine del filtro
- ftype è il tipo di filtro che si vuole realizzare
- Wn sono le frequenze di taglio normalizzate (può essere anche un solo valore)
ORDINE DEL FILTRO
L'ordine del filtro è legato alla selettività del filtro, ovvero a quanto repentinamente scende la risposta in frequenza
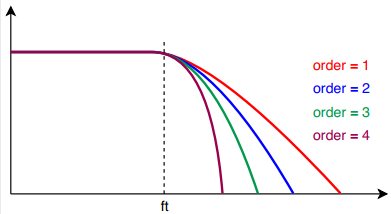
l'ordine del filtro n è un valore maggiore o uguale a 1.
TIPO DI FILTRO
Le tipologie di filtro più comuni sono:
- Passa-Basso: passano le frequenze minori della frequenza di taglio
- Passa-Alto: passano le frequenze maggiori della frequenza di taglio
- Passa-Banda: passano le frequenze attorno alla frequenza di taglio
- Elimina-Banda: passano tutte le frequenze tranne quelle attorno alla frequenza di taglio
la stringa ftype può assumere i seguenti valori:
- 'low' specifica un filtro passa-basso con frequenza di taglio Wn. 'low' è l'impostazione predefinita per scalare Wn.
- 'high' specifica un filtro passa-alto con frequenza di taglio Wn.
- 'bandpass' specifica un filtro passa-banda se Wn è un vettore a due elementi. 'bandpass' è l'impostazione predefinita quando Wn ha due elementi.
- 'stop' specifica un filtro elimina-banda se Wn è un vettore a due elementi.
- 'DC-0' specifica che la prima banda di un filtro multibanda è una banda di arresto. 'DC-0' è l'impostazione predefinita quando Wn ha più di due elementi.
- 'DC-1' specifica che la prima banda di un filtro multibanda è una banda passante.
FREQUENZE DI TAGLIO NORMALIZZATE
Wn è un valore scalare o un vettore che rappresenta le frequenze di taglio normalizzate. La normalizzazione avviene dividendo le frequenze di taglio per Fc/2 dove Fc è la frequenza di campionamento. Per esempio se il filtro deve avere la frequenza di taglio Ft = 2000 Hz e la frequenza di campionamento è Fc = 44100 Hz la frequenza di taglio normalizzata sarà Ftn = Ft / (Fc/2) = 0.0907.
Se Wn è uno scalare, allora fir1 progetta un filtro passa-basso o passa-alto con frequenza di taglio Wn. La frequenza di taglio è la frequenza alla quale il guadagno normalizzato del filtro è di –6 dB.
Se Wn è il vettore a due elementi [w1 w2], dove w1 w2, allora fir1 progetta un filtro passa-banda o elimina-banda con una frequenza di taglio più bassa w1 e una frequenza di taglio più alta w2.
Se Wn è il vettore a più elementi [w1 w2 ... wn], dove w1 < w2 < ... < wn, allora fir1 restituisce un filtro multibanda di ordine n con bande 0 < ω < w1, w1 < ω < w2, ..., wn < ω < 1.
Ad esempio, per realizzare un filtro FIR passa-basso con frequenza di taglio Ft = 2000 Hz del 10 ordine sarà necessario digitare:
>> Fc = 44100;
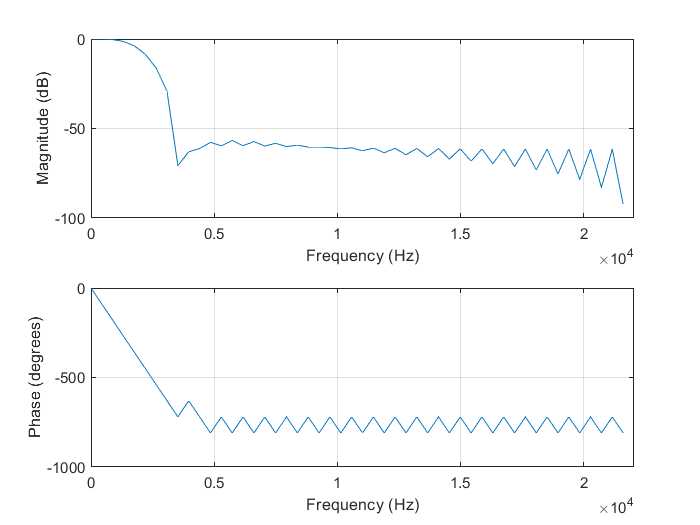
La funzione freqz() usata mostra la risposta in frequenza del filtro digitale. Si osserva che già a circa 2.5 KHz l'ampiezza delle armoniche è attenuata di 50 dB (più di 300 volte) e che la fase è lineare almeno fino a quella frequenza. Si ha quindi che le condizioni di Heaviside sono rispettate e il filtro non introduce distorsione.
L'm-file seguente mostra invece come il filtro progettato precedentemente può essere utilizzato per filtrare un segnale composto da due toni, uno a 1000 Hz e un secondo a 8000 Hz. Si farà uso anche della trasformata di Fourier per vedere lo spettro dei segnali e della funzione sound() per constatare la bontà del filtraggio.
clear;close all;Fc = 44100; % Frequenza di campionamento (44100 Hz)F1 = 1000; % Frequenza del primo tono generato (1 KHz)F2 = 8000; % Frequenza del secondo tono generato (8 KHz)t = (0:1/Fc 200000-1)/Fc).'; % Asse dei tempi con 200000 campioni (vettore colonna)
200000-1)/Fc).'; % Asse dei tempi con 200000 campioni (vettore colonna)xm = sin(2*pi*F1*t)+sin(2*pi*F2*t); % Generazione segnale monocanale (vettore colonna)x = [xm xm]; % Generazione segnale stereofonico (matrice con 2 colonne)sound(x, Fc); % Suona nella periferica audioX = fft(x); % Calcolo della fft[Ncampioni Ncanali] = size(X);X = 1/Ncampioni*fftshift(X);P = abs(X).^2; % PeriodogrammaP = P./max(max(P)); % NormalizzazioneP = 10*log10(P); % Periodigramma in dBdF = Fc/Ncampioni;f = -Fc/2:dF:Fc/2-dF; % Asse delle frequenzefigure;subplot(2,1,1);plot(f,P(:,1));ylabel('Canale SX [dB]');axis([0 15000 -150 0]);grid on;title('Periodigramma segnale di partenza');subplot(2,1,2);plot(f,P(:,2));xlabel('Frequenza [Hz]');ylabel('Canale DX [dB]');axis([0 15000 -150 0]);grid on;disp('Premi un tasto per continuare');pause();Ft = 1000; % Frequenza di taglio del filtro passa bassoFtn = Ft/(Fc/2); % Frequenza di taglio normalizzatan = 50; % Ordine del filtrob = fir1(n, Ftn, 'low'); % Realizzazione del filtroa = 1; % Nei filtri fir a=1 semprefigure;freqz(b,a,n,Fc); % Grafico della risposta del filtrogrid on;title('Caratteristiche del filtro');x1 = filter(b,a,x); % Filtraggio del segnalesound(x1, Fc); % Suona nella periferica audioX1 = fft(x1); % Calcolo della fft[Ncampioni Ncanali] = size(X1);X1 = 1/Ncampioni*fftshift(X1);P1 = abs(X1).^2; % PeriodogrammaP1 = P1./max(max(P1)); % NormalizzazioneP1 = 10*log10(P1); % Periodigramma in dBdF = Fc/Ncampioni;f = -Fc/2:dF:Fc/2-dF; % Asse delle frequenzefigure;subplot(2,1,1);plot(f,P1(:,1));ylabel('Canale SX [dB]');axis([0 15000 -150 0]);grid on;title('Periodigramma segnale filtrato');subplot(2,1,2);plot(f,P1(:,2));xlabel('Frequenza [Hz]');ylabel('Canale DX [dB]');axis([0 15000 -150 0]);grid on;